|
|
|
$$2p = S \times 4$$
Perimeter
$$S = \frac{2p}{4}$$
$$A = {S}^{2}$$
Area
$$S = \sqrt{A}$$
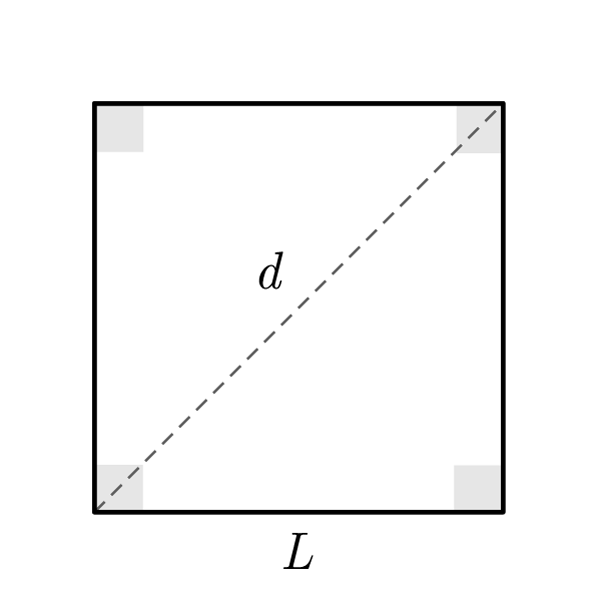
$$d = S \sqrt{2}$$
Diagonal
$$S = \frac{d}{\sqrt{2}}$$
$$A = \frac{{d}^{2}}{2}$$
Area
$$d = \sqrt{2A}$$
Definition
A square is a polygon with four sides and four congruent angles (right angles).
Properties
- Four congruent sides
- Four congruent right angles
- Diagonals are perpendicular
- The diagonal makes two right congruent triangles. In particular every triangle has angles of 45°, 45°, 90°
Square Formulas
| Data | Formula |
|---|---|
| Perimeter | 2p = S × 4 |
| Area | A = S2 |
| Side | S = 2p / 4 |
| Side | S = √A |
| Diagonal | d = S × √2 |
| Side | S = d / √2 |
| Area | A = d2 / 2 |
| Diagonal | d = √(2A) |