|
|
|
$$2p = i + c_{1} + c_{2}$$
Perimeter
$$A = \frac{c_{1} \times c_{2}}{2}$$
Area
$$c_{1} = \frac{A \times 2}{c_{2}}$$
$$c_{2} = \frac{A \times 2}{c_{1}}$$
$$A = \frac{i \times h}{2}$$
Area
$$i = \frac{A \times 2}{h}$$
$$h = \frac{A \times 2}{i}$$
Pythagoras' theorem
$$i = \sqrt{ {c_{1}}^2 + {c_{2}}^2 }$$
Pythagoras' theorem
$$c_{1} = \sqrt{ {i}^2 - {c_{2}}^2 }$$
$$c_{2} = \sqrt{ {i}^2 - {c_{1}}^2 }$$
$$i : c_{1} = c_{1} : p_{1}$$
$$i : c_{2} = c_{2} : p_{2}$$
$$p_{1} : h = h : p_{2}$$
Isosceles Right Triangle
$$i = c \sqrt{2}$$
$$c = \frac{i}{\sqrt{2}}$$
$$A = \frac{{c}^2}{2}$$
$$A = \frac{{i}^2}{4}$$
$$c = \sqrt{2A}$$
Right Triangle 30, 60, 90°
$$i = c_{1} \times 2$$
Hypotenuse
$$c_{1} = \frac{i}{2}$$
Minimum Cathetus
$$c_{2} = c_{1} \sqrt{3}$$
Maximum Cathetus
$$c_{1} = \frac{c_{2}}{\sqrt{3}}$$
Minimum Cathetus
$$c_{2} = i \frac{\sqrt{3}}{2}$$
Maximum Cathetus
$$i = c_{2} \frac{2}{\sqrt{3}}$$
Hypotenuse
Definition
The right triangle is a triangle with a right angle (90 degree).
Properties
- It has a right angle (90 degree)
- The Pythagoras' theorem is valid
- All the Generic Triangle formulas are valid
- It can be inscribed inside a semicircle where the radius is half the hypotenuse
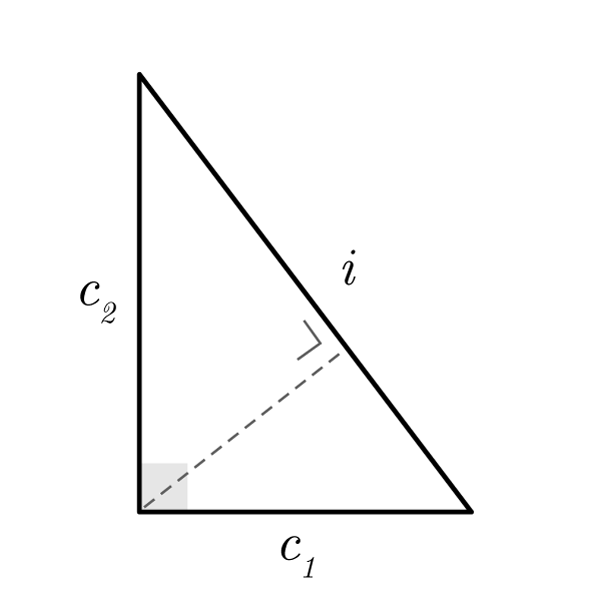
Right Triangle Formulas
| Data | Formula |
|---|---|
| Perimeter | 2p = i + c1 + c2 |
| Area | A = (c1 × c2) / 2 |
| Area | A = (i × h) / 2 |
| Hypotenuse | i = √( c12 + c22 ) |
| Minimum Cathetus | c1 = √( i2 - c22 ) |
| Maximum Cathetus | c2 = √( i2 - c12 ) |
| Minimum Cathetus | c1 = (A × 2) / c2 |
| Maximum Cathetus | c2 = (A × 2) / c1 |
| Hypotenuse | i = (A × 2) / h |
| Height | h = (A × 2) / i |
Isosceles Right Triangle Formulas
| Data | Formula |
|---|---|
| Hypotenuse | i = c √2 |
| Cathetus | c = i / (√2) |
| Area | A = c2 / 2 |
| Area | A = i2 / 4 |
| Cathetus | c = √(2A) |
Right Triangle 30, 60, 90° Formulas
| Data | Formula |
|---|---|
| Hypotenuse | i = c1 × 2 |
| Minimum Cathetus | c1 = i / 2 |
| Maximum Cathetus | c2 = c1 √3 |
| Minimum Cathetus | c1 = c2 / (√3) |
| Maximum Cathetus | c2 = i (√3 / 2) |
| Hypotenuse | i = c2 (2 / √3) |