|
|
|
$$2p = 2a+2b$$
Perimeter
$$A = a \times b$$
Area
$$a = \frac{A}{b}$$
Length
$$b = \frac{A}{a}$$
Width
$$d = \sqrt{{a}^{2} + {b}^{2}}$$
Diagonal (Pythagoras' theorem)
$$a = \sqrt{{d}^{2} - {b}^{2}}$$
Length
$$b = \sqrt{{d}^{2} - {a}^{2}}$$
Width
Definition
A rectangle is a quadrilateral with internal angles congruent (right angles) and opposite sides congruent.
Properties
- One side is larger (length) and the other smaller (width). The opposite sides are congruent (the sides are congruent in group of two)
- The sides can be also written as base (length) and height (width)
- Four congruent right angles
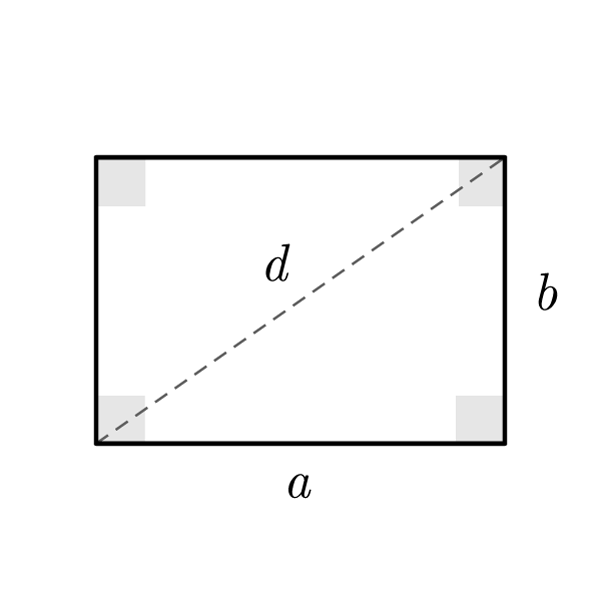
Rectangle Formulas
| Data | Formula |
|---|---|
| Perimeter | 2p = 2 × a + 2 × b |
| Area | A = a × b |
| Diagonal | d = √( a2 + b2 ) |
| Length | a = A / b |
| Width | b = A / a |
| Length | a = √( d2 - b2 ) |
| Width | b = √( d2 - a2 ) |