|
|
|
$$V = \frac{A_{base} \times h}{3}$$
Volume
$$A_{base} = \frac{3V}{h}$$
Base area
$$h = \frac{3V}{A_{base}}$$
Height
$$S_{tot} = A_{base} + S_{lat}$$
Total surface
$$S_{lat} = S_{tot} - A_{base}$$
Lateral surface
$$A_{base} = S_{tot} - S_{lat}$$
Base area
Right Pyramid
$$S_{lat} = \frac{2p \times a}{2}$$
Lateral surface
$$2p = \frac{2 \times S_{lat}}{a}$$
Base perimeter
$$a = \frac{2 \times S_{lat}}{2p}$$
Apothem
$$r = \frac{2 \times A_{base}}{2p}$$
Inscribed radius
$$2p = \frac{2 \times A_{base}}{r}$$
Base perimeter
$$A_{base} = \frac{2p \times r}{2}$$
Base area
By using the Pythagoras' Theorem
$$a = \sqrt{{h}^2 + {r}^2}$$
Apothem
$$r = \sqrt{{a}^2 - {h}^2}$$
Base radius
$$h = \sqrt{{a}^2 - {r}^2}$$
Height
Quadrangular Pyramid
$$A_{base} = {S}^2$$
Base area
$$S = \sqrt{A_{base}}$$
Base Edge
$$2p = S \times 4$$
Base perimeter
$$S = \frac{2p}{4}$$
Base Edge
$$r = \frac{S}{2}$$
Base radius
$$S = 2 r$$
Base Edge
Definition
A pyramid is a polyhedron formed by a polygonal face, called base, and a point external to the base, called vertex.
Properties
- In a pyramid there is a base face and lateral faces
- The lateral face of a pyramid are isosceles triangles congruent to each other
- Height: perpendicular segment that connects the vertex of the pyramid with the plane that contains the base
- Apothem: in the regular pyramid, segment that joins the vertex with the midpoint of the base edge. It coincides with the height of one of the triangles that make up the lateral faces
Other definitions
- A right pyramid is a pyramid in which the base polygon is inscribed in a circle, and the height joins the vertex with the center of the inscribed circle
- An oblique pyramid is any pyramid that is not a right pyramid
- A regular pyramid is a pyramid having a regular polygon as its base
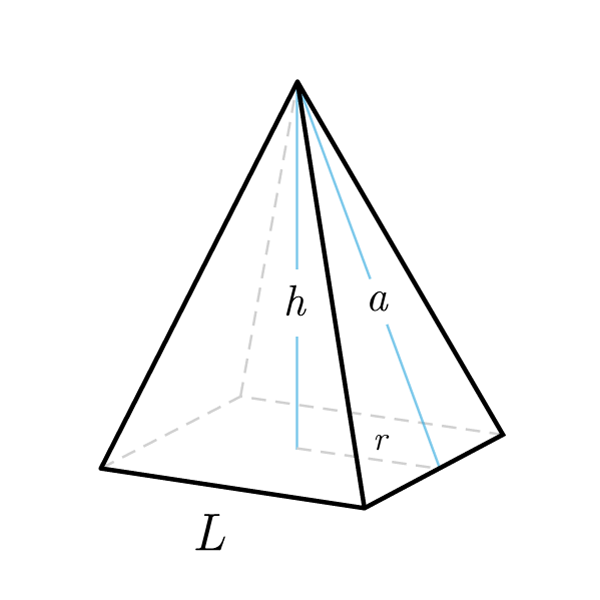
Pyramid Formulas
| Data | Formula |
|---|---|
| Volume | V = (Abase × h) / 3 |
| Base area | Abase = (3V) / h |
| Height | h = (3V) / Abase |
| Total surface | Stot = Abase + Slat |
| Lateral surface | Slat = Stot - Abase |
| Base area | Abase = Stot - Stot |
Right Pyramid Formulas
| Data | Formula |
|---|---|
| Lateral surface | Stot = (2p × a) / 2 |
| Base perimeter | 2p = (2 × Slat) / a |
| Apothem | a = (2 × Slat) / 2p |
| Inscribed radius | r = (2 × Abase) / 2p |
| Base perimeter | 2p = (2 × Abase) / r |
| Base area | Abase = (2p × r) / 2 |
| Apothem | a = √(h2 + r2) |
| Base radius | r = √(a2 - h2) |
| Height | h = √(a2 - r2) |
Quadrangular Pyramid Formulas
| Data | Formula |
|---|---|
| Lateral surface | Abase = S2 |
| Base Edge | S = √(Abase) |
| Base perimeter | 2p = S × 4 |
| Base Edge | S = (2p) / 2 |
| Base radius | r = S/2 |
| Base Edge | S = 2r |