|
|
|
$$2p = S \times 5$$
Perimeter
$$S = \frac{2p}{5}$$
$$A = \frac{2p \times a}{2}$$
Area
$$a = \frac{2A}{2p}$$
Apothem
$$2p = \frac{2A}{a}$$
Perimeter
$$d = \frac{S (\sqrt{5} + 1)}{2}$$
Diagonal
$$S = \frac{d (\sqrt{5} - 1)}{2}$$
Side
Fixed number
$$f = 0.688 = \frac{a}{S}$$
Fixed number
$$a = S \times f$$
Apothem
$$S = \frac{a}{f}$$
Side
Area's costant
$$\varphi = 1.720 = \frac{A}{{S}^2}$$
Area's costant
$$A = {S}^2 \times \varphi$$
Area
$$S = \sqrt{\frac{A}{\varphi}}$$
Side
Inscribed Pentagon
$$S = \frac{ R\sqrt{10 - 2 \sqrt{5}} }{2}$$
Side
$$a = \frac{ R \times \left( \sqrt{5} + 1 \right) }{2}$$
Apothem
$$A = \frac{ {R}^2 \times 5 \sqrt{ 10 + 2 \sqrt{5} } }{8}$$
Area
$$R = d \left[ \sqrt{ \frac{5 - \sqrt{5}}{10} } \right]$$
Circumcircle's Radius
$$d = R \left[ \sqrt{ \frac{5 + \sqrt{5}}{2} } \right]$$
Diagonal
Definition
A pentagon is a polygon with five sides. A regular pentagon is a regular polygon with five sides and five angles congruent.
Properties
- Polygon with five sides
- The regular pentagon has five sides and five angles congruent, with a measure of 108°
- A regular pentagon can be inscribed into a circle or circumscribed by a circle
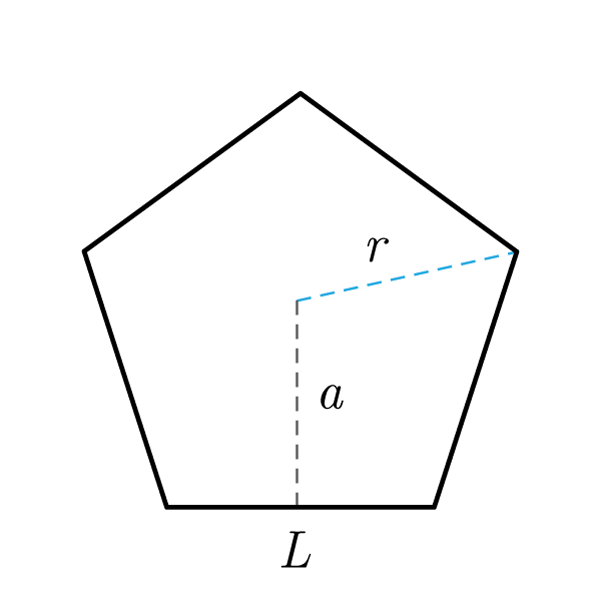
Pentagon Formulas
| Data | Formula |
|---|---|
| Perimeter | 2p = S × 5 |
| Area | A = (2p × a) / 2 |
| Diagonal | d = [S(√5 + 1)] / 2 |
| Side | S = 2p / 5 |
| Fixed number | f = 0.688 = a / S |
| Area's costant | φ = 1.720 = A / (S2) |
| Apothem | a = (2A) / (2p) |
| Perimeter | 2p = (2A) / (a) |
| Side | S = [d(√5 - 1)] / 2 |
| Apothem | a = S × f |
| Side | S = a / f |
| Area | A = S2 × φ |
| Side | S = √(A / φ) |