|
|
|
$$2p = b + S \times 2$$
Perimeter
$$b = 2p - S \times 2$$
$$S = \frac{2p - b}{2}$$
$$A = \frac{b \times h}{2}$$
Area
$$b = \frac{A \times 2}{h}$$
$$h = \frac{A \times 2}{b}$$
$$S = \sqrt{ {h}^2 + {\left(\dfrac{b}{2}\right)}^2 }$$
Oblique Side (Pythagoras' theorem)
$$h = \sqrt{ {S}^2 - {\left(\dfrac{b}{2}\right)}^2 }$$
$$b = \sqrt{ {S}^2 - {h}^2 } \times 2$$
Definition
An isosceles triangle is a triangle with two congruent sides.
Properties
- Two congruent sides
- Base angles are congruent
- All the Generic Triangle formulas are valid
- The height relative to the base divides the shape in two congruent right triangles. For these are valid the Right Triangle formulas
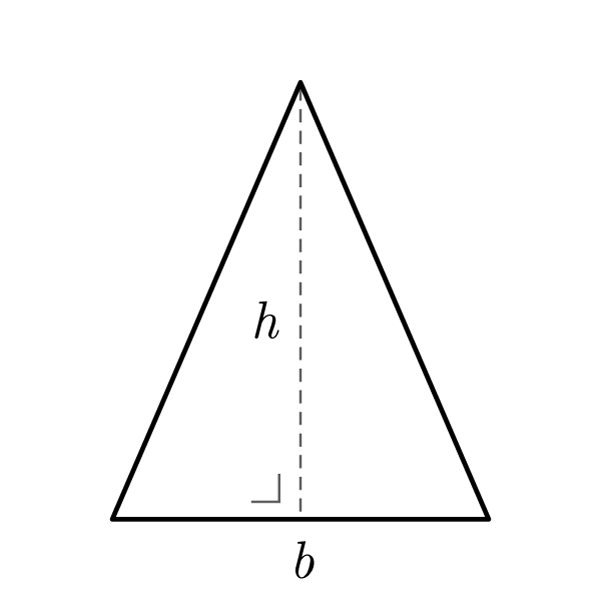
Isosceles Triangle Formulas
| Data | Formula |
|---|---|
| Perimeter | 2p = b + S × 2 |
| Area | A = (b × h) / 2 |
| Oblique Side | S = √[ h2 + (b / 2)2 ] |
| Base | b = (A × 2) / h |
| Height | h = (A × 2) / b |
| Base | b = 2p - S × 2 |
| Side | S = (2p - b) / 2 |
| Height | h = √[ S2 - (b / 2)2 ] |
| Base | b = √( S2 - h2 ) × 2 |