|
|
|
$$2p = S \times 4$$
Perimeter
$$S = \frac{2p}{4}$$
$$A = \frac{d_{1} \times d_{2}}{2}$$
Area
$$d_{1} = \frac{2A}{d_{2}}$$
Longer Diagonal
$$d_{2} = \frac{2A}{d_{1}}$$
Shorter Diagonal
$$S = \sqrt{ {\left(\frac{d_{1}}{2}\right)}^{2} + {\left(\frac{d_{2}}{2}\right)}^{2} }$$
Side (Pythagoras' theorem)
$$\frac{d_{1}}{2} = \sqrt{ {S}^{2} - {\left(\frac{d_{2}}{2}\right)}^{2} }$$
Longer Semi-Diagonal
$$\frac{d_{2}}{2} = \sqrt{ {S}^{2} - {\left(\frac{d_{1}}{2}\right)}^{2} }$$
Shorter Semi-Diagonal
Definition
A rhombus is a quadrilater with all sides congruent.
Properties
- Four congruent sides, opposite sides are parallel
- Opposite angles are congruent, consecutive angles are supplementary (their sum is 180°)
- Diagonals are perpendicular
- Diagonals meet at a point called rhombus' center. The center divides the diagonals into two equal semi-diagonals
- Diagonals makes four congruent right triangles, in which the hypotenuse is represented by the rhombus' side, and the cathetus' by the semi-diagonals
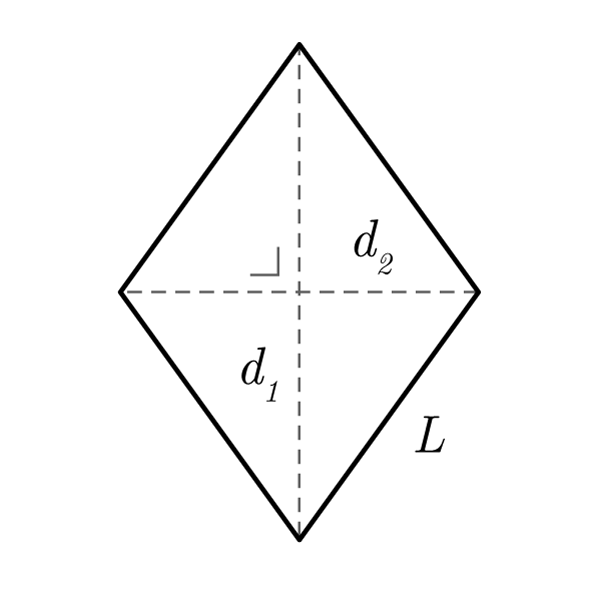
Rhombus Formulas
| Data | Formula |
|---|---|
| Perimeter | 2p = S× 4 |
| Area | A = (d1 × d2) / 2 |
| Side | S = 2p / 4 |
| Side | S = √[ (d1 / 2)2 + (d2 / 2)2 ] |
| Longer Diagonal | d1 = (2 × A) / d2 |
| Shorter Diagonal | d2 = (2 × A) / d1 |
| Longer Semi-Diagonal | d1 / 2 = √[ S2 - (d2 / 2)2 ] |
| Shorter Semi-Diagonal | d2 / 2 = √[ S2 - (d1 / 2)2 ] |