|
|
|
$$2p = S \times 3$$
Perimeter
$$A = \frac{S \times h}{2}$$
Area
$$S = \frac{A \times 2}{h}$$
$$h = \frac{A \times 2}{S}$$
$$S = \frac{2p}{3}$$
Side
Knowing side or height only
$$2p = 2 h \sqrt{3}$$
Perimeter (with height)
$$h = \frac{2p}{2\sqrt{3}}$$
Height (from perimeter)
$$A = \frac{\sqrt{3}}{4} {S}^2$$
Area (with side)
$$A = \frac{{h}^2}{\sqrt{3}}$$
Area (with height)
$$S = \frac{2h}{\sqrt{3}}$$
Side (with height)
$$h = \frac{S\sqrt{3}}{2}$$
Height (with side)
Inscribed circumference
$$r = \frac{1}{2 \sqrt{3}} S$$
Inscribed radius (with side)
$$r = \frac{1}{3} h$$
Inscribed radius (with height)
$$S = 2r\sqrt{3}$$
Side
$$h = 3r$$
Height
$$2p = 6r\sqrt{3}$$
Perimeter
$$A = 3{r}^2 \sqrt{3}$$
Area
Circumscribed circumference
$$R = \frac{\sqrt{3}}{3} S$$
Circumscribed radius (with side)
$$R = \frac{2}{3} h$$
Circumscribed radius (with side)
$$S = R\sqrt{3}$$
Side
$$h = \frac{3}{2}R$$
Height
$$2p = 3\sqrt{3}R$$
Perimeter
$$A = \frac{3\sqrt{3}}{4}{R}^2$$
Area
Definition
An equilateral triangle is a triangle with all sides congruent.
Properties
- All sides are congruent
- All angles are congruent
- All the Generic Triangle formulas are valid
- The height relative to the base divides the shape in two congruent right triangles. For these are valid the Right Triangle formulas
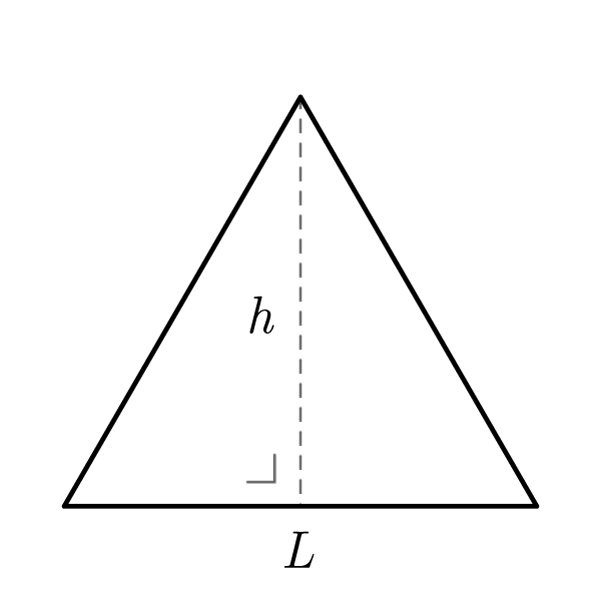
Equilateral Triangle Formulas
| Data | Formula |
|---|---|
| Perimeter | 2p = S × 3 |
| Area | A = (S × h) / 2 |
| Side | S = 2p / 3 |
| Side (with height) | S = (2 × h) / √3 |
| Height (with side) | h = (S√3) / 2 |
| Height (from perimeter) | h = 2p / (2√3) |
| Perimeter (with height) | A = 2 × h × √3 |
| Area (with side) | A = (√3 / 4) × S2 |
| Area (with height) | A = h2 / √3 |
| Side | S = (A × 2) / h |
| Height | h = (A × 2) / S |
Equilateral Triangle - Inscribed circumference
| Data | Formula |
|---|---|
| Inscribed radius (with side) | r = [1 / (2√3)] × S |
| Inscribed radius (with height) | r = 1/3 × h |
| Side | S = 2r√3 |
| Height | h = 3r |
| Perimeter | 2p = 6r√3 |
| Area | A = 3r2√3 |
Equilateral Triangle - Circumscribed circumference
| Data | Formula |
|---|---|
| Circumscribed radius (with side) | r = (√3 / 3) × S |
| Circumscribed radius (with height) | r = 2/3 × h |
| Side | S = R√3 |
| Height | h = 3/2 × R |
| Perimeter | 2p = 3√3R |
| Area | A = [(3√3) / 4] × R2 |