|
|
|
$$V = {S}^3$$
Volume
$$S = \sqrt[3]{V}$$
Edge
$$D = S\sqrt{3}$$
Cube diagonal
$$S = \frac{D}{\sqrt{3}}$$
Edge
$$A_{base} = {S}^{2}$$
Base area
$$S = \sqrt{A_{base}}$$
Edge
$$d = S\sqrt{2}$$
Base diagonal
$$S = \frac{d}{\sqrt{2}}$$
Edge
Total surface
$$S_{tot} = A_{base} + 2S_{lat}$$
Total surface
$$S_{tot} = 6{S}^{2}$$
Total surface
$$S_{tot} = 6A_{base}$$
Total surface
$$S = \sqrt{\frac{S_{tot}}{6}}$$
Edge
$$S_{tot} = 2{D}^{2}$$
Total surface
$$D = \sqrt{\frac{S_{tot}}{2}}$$
Cube diagonal
Lateral surface
$$S_{lat} = S_{tot} - 2A_{base}$$
Lateral surface
$$S_{lat} = 4{S}^{2}$$
Lateral surface
$$S = \sqrt{\frac{S_{lat}}{4}}$$
Edge
Cube inscribed into a sphere
$$R = \frac{\sqrt{3}}{2}S$$
Circumscribed radius
$$S = \frac{2}{\sqrt{3}}R$$
Edge
Cube circumscribed to a sphere
$$r = \frac{S}{2}$$
Inscribed radius
$$S = 2r$$
Edge
Radiuses relation
$$R = r\sqrt{3}$$
Circumscribed radius
$$r = \frac{R}{\sqrt{3}}$$
Inscribed radius
Definition
A cube, or regular hexahedron, is a polyhedron bounded by 6 square faces, 8 vertices and 12 edges.
Properties
- 6 congruent square faces, perpendicular to two by two to each other
- A cube is a regular hexahedron. A hexahedron is any polyhedron with six faces
- All the Square formulas are valid
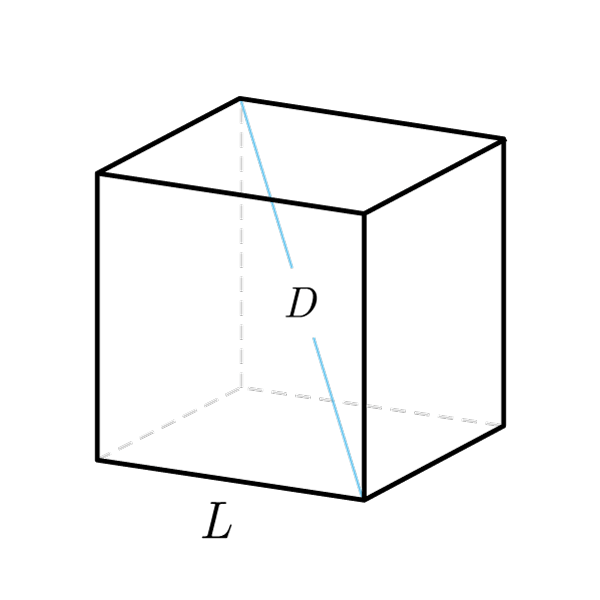
Cube Formulas
| Data | Formula |
|---|---|
| Volume | V = S3 |
| Edge | S = 3√(V) |
| Cube diagonal | D = S√3 |
| Edge | S = D / (√3) |
| Base area | Abase = S2 |
| Edge | S = √(Abase) |
| Base diagonal | d = S√2 |
| Edge | S = d / √2 |
| Total surface | Stot = Abase + 2 × Slat |
| Total surface | Stot = 6S2 |
| Total surface | Stot = 6 × Abase |
| Edge | S = √(Stot / 6) |
| Total surface | Stot = 2D2 |
| Cube diagonal | D = √(Stot / 2) |
| Lateral surface | Slat = Stot - 2 × Abase |
| Lateral surface | Slat = 4S2 |
| Edge | S = √(Slat / 4) |
Cube inscribed into a sphere
| Data | Formula |
|---|---|
| Circumscribed radius | R = (√3/2) × S |
| Edge | S = (2/√3) × R |
Cube circumscribed to a sphere
| Data | Formula |
|---|---|
| Inscribed radius | R = S/2 |
| Edge | S = 2r |
Radiuses relation
| Data | Formula |
|---|---|
| Circumscribed radius | R = r√3 |
| Inscribed radius | r = R/√3 |