|
|
|
$$V = \frac{\pi {r}^{2} h}{3}$$
Volume
$$r = \sqrt{\frac{3 V}{\pi h}}$$
Radius
$$h = \frac{3 V}{\pi {r}^{2}}$$
Height
$$V = \frac{A_{base} h}{3}$$
Volume
By using the Pythagoras' Theorem
$$a = \sqrt{{h}^2 + {r}^2}$$
Apothem
$$h = \sqrt{{a}^2 - {r}^2}$$
Height
$$r = \sqrt{{a}^2 - {h}^2}$$
Radius
Lateral surface
$$S_{tot} = A_{base} + S_{lat}$$
Total surface
$$S_{lat} = S_{tot} - A_{base}$$
Lateral surface
$$S_{lat} = \pi r a$$
Lateral surface
$$r = \frac{S_{lat}}{\pi a}$$
Radius
$$r = \frac{S_{lat}}{\pi r}$$
Apothem
$$A_{base} = \pi {r}^2$$
Base area
$$A_{base} = S_{tot} - S_{lat}$$
Base area
Other formulas
$$2 r = a$$
Equilateral cone
Definition
A cone is a solid of rotation which is obtained by rotating a right triangle around one of cathetus.
Properties
- In a cone - the radius, height and apothem form a right triangle
- A cone is equivalent (has the same volume) to one third of a cylinder having the same length and radius and height as those of the cone
- An equilateral cone is a cone in which the diameter and the apothem have the same length
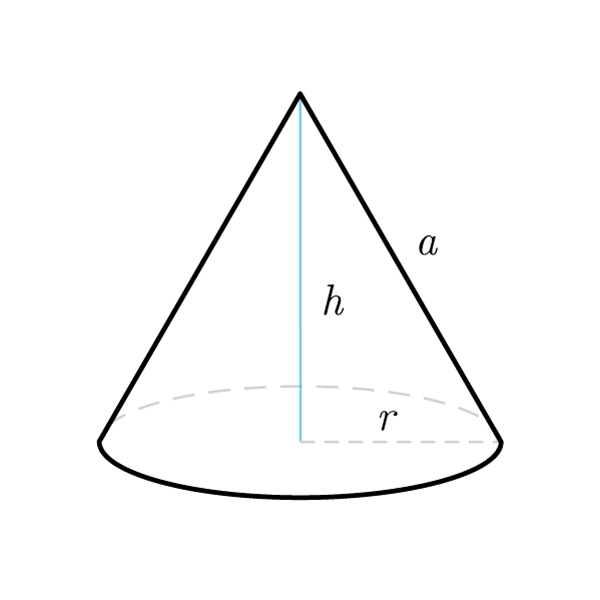
Cone Formulas
| Data | Formula |
|---|---|
| Volume | V = (π r2 h) / 3 |
| Radius | V = √[ (3V) / (π h) ] |
| Height | h = (3V) / (π r2) |
| Volume | V = (Abase × h) / 3 |
| Apothem | a = √(h2 + r2) |
| Height | h = √(a2 - r2) |
| Radius | r = √(a2 - h2) |
| Total surface | Stot = Abase + Slat |
| Lateral surface | Slat = Stot - Abase |
| Lateral surface | Slat = π r a |
| Radius | r = Slat / (π a) |
| Apothem | a = Slat / (π r) |
| Base area | Abase = π r2 |
| Base area | Abase = Stot - Slat |